
Les formules mathématiques
Secondaire 1-5
|
Arithmétique et algèbre |
Géométrie | Géométrie analytique | Probabilités et statistique |
|---|---|---|---|
|
Exprimer un nombre en pourcentage Les fonctions exponentielles et logarithmiques |
La conversion des unités de mesure Le périmètre et l'aire de figures planes Les mesures dans les polygones L'aire et le volume des solides Les mesures dans les triangles rectangles |
Les droites dans le plan cartésien |
Arithmétique et algèbre
Exprimer un nombre en pourcentage (Sec. 1-2)
|
numérateurdénominateur×100 |
numérateurdénominateur=nombre recherché100 |
Les propriétés des opérations (Sec. 1-2)
|
Propriétés |
Addition |
Multiplication |
|---|---|---|
|
a+b=b+a |
a×b=b×a |
|
(a+b)+c=a+(b+c) |
(a×b)×c=a×(b×c) |
|
a+0=0+a=a |
a×1=1×a=a |
|
|
a×0=0×a=0 |
|
a+−a=−a+a=0 |
a×1a=1 |
|
a×(b±c)=a×b±a×c |
|
Les fonctions réelles (Sec. 3-4-5)
|
Fonctions |
Règles de base |
Règles transformées |
||
|---|---|---|---|---|
|
Degré 0 |
y=b |
|
||
|
Degré 1 |
y=x |
Forme |
Forme |
Forme |
|
y=ax+ba : taux de variation b : ordonnée à l'originea=y2−y1x2−x1 |
xa+yb=1a : abscisse à l'origine b : ordonnée à l'origine |
Ax+By+C=0 |
||
|
⇒ symétriqueas=−bfafbs=bf |
⇒ fonctionnelleaf=−bsasbf=bs |
⇒ fonctionnelleaf=−ABbf=−CB |
||
|
⇒ générale Dénominateur commun et mettre tout du même côté |
⇒ générale Dénominateur commun et mettre tout du même côté |
⇒ symétriqueas=−CAbs=−CB |
||
|
Degré 2 |
y=x2 |
Forme |
Forme |
Forme |
|
y=ax2+bx+c |
y=a(b(x−h))2+ky=a b2(x−h)2+ky=a(x−h)2+k |
Deux zérosy=a(x−z1)(x−z2)Un seul zéroy=a(x−z1)2 |
||
|
Nombre de zéros√b2−4ac |
Nombre de zéros√−ka |
Nombre de zéros |
||
|
Valeur des zéros−b±√b2−4ac2a |
Valeur des zérosh±√−ka |
Valeur des zéros z1 et z2 |
||
|
Valeur absolue |
y=|x| |
Forme canonique |
||
|
y=a |b(x−h)|+ky=a |b|×|x−h|+ky=a |x−h|+k |
||||
|
Racine carrée |
y=√x |
Forme canonique |
||
|
y=a√b(x−h)+ky=a√b√±(x−h)+ky=a√±(x−h)+k |
||||
| Partie entière | y=[x] | Forme canonique | ||
| y=a[b(x−h)]+k | ||||
Les fonctions exponentielles et logarithmiques (Sec. 4 CST-TS et 5 TS-SN)
|
Fonctions |
Règles de base |
Règles transformées |
Définitions et lois |
|---|---|---|---|
|
Exponentielle |
f(x)=cx |
f(x)=a(c)b(x−h)+k |
a0=1a1=aa−m=1amamn=n√amam=an ⇔ m=naman=am+naman=am−n(ab)m=ambm(am)n=amn(ab)m=ambmn√ab=n√a n√bn√ab=n√an√b |
|
Logarithme |
f(x)=logcx |
f(x)=alogc(b(x−h))+k |
logc1=0logcc=1clogcm=mlogccm=mlogcm=logcn ⇔ m=nlogc(mn)=logcm+logcnlogc(mn)=logcm−logcnlogc(mn)=nlogcmlogcm=logsmlogsc |
|
L'une est la réciproque de l'autrex=cy ⟺ y=logcx |
|||
Les fonctions trigonométriques (Sec. 5 TS-SN)
|
Fonctions |
Règles de base |
Règles transformées |
Particularités |
|---|---|---|---|
|
Sinus |
f(x)=sinx |
f(x)=asin(b(x−h))+k |
|a|=max−min2|b|=2πpériodeImaf=[k−a,k+a]Zéros : Une infinité de la forme (x1+nP) et (x2+nP) où x1 et x2 sont des zéros consécutifs, n∈Z et P est la période. |
|
Cosinus |
f(x)=cosx |
f(x)=acos(b(x−h))+k |
|
|
Tangente |
f(x)=tanx |
f(x)=atan(b(x−h))+k |
|b|=πpériodeDom f=R∖{(h+P2)+nP}où n∈Z et P est la période. Zéros : Une infinité de la forme x1+nP où x1 est un zéro, n∈Z et P est la période. |
|
Arc sinus |
f(x)=arcsin(x)ouf(x)=sin−1(x) |
f(x)=aarcsin(b(x−h))+k |
|
|
Arc cosinus |
f(x)=arccos(x)ouf(x)=cos−1(x) |
f(x)=aarccos(b(x−h))+k |
|
|
Arc tangente |
f(x)=arctan(x)ouf(x)=tan−1(x) |
f(x)=aarctan(b(x−h))+k |
|
Les identités trigonométriques (Sec. 5 TS-SN)
|
Identités de base |
|||||
|---|---|---|---|---|---|
|
sin2θ+cos2θ=1 |
1+tan2θ=sec2θ |
1+cotan2θ=cosec2θ |
|||
|
Autres identités |
|||||
|
sin(a+b)=sinacosb+cosasinbsin(a−b)=sinacosb−cosasinbcos(a+b)=cosacosb−sinasinbcos(a−b)=cosacosb+sinasinbtan(a+b)=tana+tanb1−tanatanbtan(a−b)=tana−tanb1+tanatanb |
sin2x=2sinxcosxcos2x=1−2sin2xtan2x=2cotanx−tanxsin(−θ)=−sinθcos(−θ)=cosθsin(θ+π2)=cosθcos(θ+π2)=−sinθ |
||||
Géométrie
La conversion des unités de mesure (Sec. 1-2-3)
| km | hm | dam | m | dm | cm | mm |
| Dans ce sens ⇒×10 Dans ce sens ⇐÷10 | ||||||
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| Dans ce sens ⇒×100 Dans ce sens ⇐÷100 | ||||||
| km3 | hm3 | dam3 | m3 | dm3 | cm3 | mm3 |
| Dans ce sens ⇒×1000 Dans ce sens ⇐÷1000 | ||||||
Le périmètre et l'aire des figures planes (Sec. 1-2-4)
|
Figures |
Périmètre |
Aire |
|
|---|---|---|---|
|
Triangle |
La somme de tous les côtés |
A=b×h2 |
|
|
Carré |
P=4×c |
A=c×cA=c2 |
|
|
Rectangle |
P=b+h+b+hP=2(b+h) |
A=bh |
|
|
Losange |
P=4×c |
A=D×d2 |
|
|
Parallélogramme |
La somme de tous les côtés |
A=bh |
|
|
Trapèze |
La somme de tous les côtés |
A=(B+b)×h2 |
|
|
Polygone régulier |
P=n×c |
A=can2
|
|
|
Polygones quelconque |
La somme de tous les côtés |
Décomposer le polygone en plusieurs polygones connus et additionner les aires de ces polygones. |
|
|
Disque et cercle |
d=2rr=d2 |
C=πdC=2πr |
A=πr2 |
|
Arc de cercle et secteur de disque |
Angle au centre360o=Mesure d'arc2πr |
Angle au centre360o=Aire du secteurπr2 |
|
Les mesures dans le cercle (Sec. 1-2 et 5 TS)
|
Les théorèmes dans le cercle |
|---|
|
Les théorèmes en lien avec les rayons, les diamètres, les cordes et les arcs :
Les théorèmes en lien avec les angles :
Les théorèmes en lien avec les sécantes et les tangentes au cercle :
|
Les mesures dans les polygones (Sec. 1-2)
|
Nombre total de diagonales |
Nombre de diagonales à chaque sommet |
Somme des mesures des angles intérieurs |
Mesure d'un angle intérieur |
|---|---|---|---|
|
n(n−3)2 |
n−3 |
180(n−2) |
180(n−2)n |
L'aire et le volume des solides (Sec. 2-3)
|
Solides |
Aire latérale |
Aire totale |
Volume |
|---|---|---|---|
|
Prisme et cylindre |
Somme des aires des faces latérales du solide AL=Pb×h |
Somme des aires de toutes les faces du solide AT=AL+2Ab |
V=Ab×h |
|
Pyramide et cône |
Somme des aires des faces latérales du solide AL=Pb×a2 |
Somme des aires de toutes les faces du solide AT=AL+Ab |
V=Ab×h3 |
|
Sphère et boule |
A=4πr2 |
V=4πr33 |
|
Les mesures dans les triangles rectangles (Sec. 3-4)
|
Les théorèmes dans le triangle rectangle |
|---|
|
|
Les relations métriques dans le triangle rectangle |
|
Théorème de la hauteur relative à l'hypoténuse Dans tout triangle rectangle, la hauteur (h) issue du sommet de l'angle droit est moyenne proportionnelle entre les mesures des deux segments (m et n) qu'elle détermine sur l'hypoténuse.mh=hnouh2=mnThéorème du produit des cathètes Dans tout triangle rectangle, le produit des cathètes (a et b) est égal au produit de l'hypoténuse (c) et de sa hauteur relative (h).ch=abouh=abcThéorème de la cathète Dans tout triangle rectangle, chaque cathète (a ou b) est moyenne proportionnelle entre la longueur de sa projection sur l'hypoténuse (respectivement m et n) et l'hypoténuse entière (c).ma=acoua2=mcnc=bcoub2=nc |
Les rapports trigonométriques (Sec. 4)
|
Rapports trigonométriques |
Lois trigonométriques (triangles quelconques) |
|
|---|---|---|
| sinA=OpposéHypoténuse | cosec A=1sinA=HypoténuseOpposé | sinAa=sinBb=sinCc |
| cosA=AdjacentHypoténuse | sec A=1cosA=HypoténuseAdjacent | a2=b2+c2−2bccosAb2=a2+c2−2accosBc2=a2+b2−2abcosC |
| tanA=OpposéAdjacent | cotanA=1tanA=AdjacentOpposé | |
Les figures et les solides semblables (Sec. 3)
|
Rapport de similitude |
Rapport d'aires |
Rapport de volumes |
|---|---|---|
|
k=Longueur figure imageLongueur figure initiale |
k2=Aire figure imageAire figure initiale |
k3=Volume solide imageVolume solide initiale |
Les vecteurs (Sec. 5 TS-SN)
|
Composantes (a,b) d'un vecteur |
|||
|---|---|---|---|
|
a=‖→u‖cosθ b=‖→u‖sinθ |
Soit le vecteur →AB avec A(x1,y1) et B(x2,y2) |
||
|
Norme d'un vecteur |
|||
|
Soit le vecteur →u=(a,b) |
Soit le vecteur →AB avec A(x1,y1) et B(x2,y2) |
||
|
Orientation d'un vecteur |
|||
|
θ=tan−1(ba) |
|
||
|
Somme de deux vecteurs |
|||
|
Soit →u=(a,b) et →v=(c,d) |
‖→u+→v‖=‖→u‖+‖→v‖−2‖→u‖ ‖→v‖ cosθ |
||
|
Soustraction de deux vecteurs |
|||
|
Soit →u=(a,b) et →v=(c,d) |
‖→u+→v‖=‖→u‖+‖→v‖−2‖→u‖ ‖→v‖ cosθ |
||
|
Multiplication par un scalaire |
|||
|
Soit k un scalaire et →u=(a,b) |
|||
|
Produit scalaire |
|||
|
Si le produit scalaire est de 0, alors les vecteurs sont perpendiculaires. |
|||
|
À l'aide des composantes |
À l'aide de la norme et de l'orientation |
||
|
Propriétés de l'addition de deux vecteurs |
|||
|
1) La somme de deux vecteurs est un vecteur. |
|
||
|
2) Commutativité |
→u+→v=→v+→u |
||
|
3) Associativité |
(→u+→v)+→w=→u+(→v+→w) |
||
|
4) Existence d'un élément neutre |
→u+→0=→0+→u=→u |
||
|
5) Existence d'opposés |
→u+(−→u)=−→u+→u=→0 |
||
|
Propriétés de la multiplication par un scalaire |
|||
|
1) Le produit d'un vecteur par un scalaire est toujours un vecteur. |
|
||
|
2) Associativité |
k1(k2→u)=(k1k2)→u |
||
|
3) Existence d'un élément neutre |
1×→u=→u×1=→u |
||
|
4) Distributivité sur l'addition de vecteurs |
k(→u+→v)=k→u+k→v |
||
|
5) Distributivité sur l'addition de scalaires |
(k1+k2)→u=k1→u+k2→v |
||
|
Propriétés du produit scalaire |
|||
|
1) Commutativité |
→u⋅→v=→v⋅→u |
||
|
2) Associativité des scalaires |
k1→u⋅k2→v=k1k2(→u⋅→v) |
||
|
3) Distributivité sur une somme vectorielle |
→u⋅(→v+→w)=(→u⋅→v)+(→u⋅→w) |
||
Géométrie analytique
Les droites dans le plan cartésien (Sec. 3-4)
|
Concepts |
Formules |
|||||
|---|---|---|---|---|---|---|
|
Accroissements |
Δx=x2−x1Δy=y2−y1 |
|||||
|
Distance entre deux points |
d(A,B)=√(x2−x1)2+(y2−y1)2 |
|||||
|
Coordonnées du point de partage |
Rapport partie |
Rapport partie |
||||
|
xp=x1+rs(x2−x1)yp=y1+rs(y2−y1) |
xp=x1+rr+s(x2−x1)yp=y1+rr+s(y2−y1) |
|||||
|
Coordonnées du point milieu |
(xm,ym)=(x1+x22,y1+y22) |
|||||
|
Pente d'une droite |
a=ΔyΔx=y2−y1x2−x1 |
|||||
|
Comparaison de deux droites d'équations y=ax+b |
Parallèles |
Parallèles |
Perpendiculaires |
|||
|
a1=a2b1=b2 |
a1=a2b1≠b2 |
a1=−1a2 |
||||
Les règles des transformations géométriques et leur réciproque dans le plan cartésien (Sec. 5 TS)
|
Transformations |
Règles |
Réciproques |
|---|---|---|
|
Translation |
t(a,b):(x,y)t↦(x+a,y+b) |
t−1(a,b)=t(−a,−b):(x,y)t↦(x−a,y−b) |
|
Rotation |
r(O,90∘):(x,y)r↦(−y,x)r(O,−270∘):(x,y)r↦(−y,x)r(O,180∘):(x,y)r↦(−x,−y)r(O,−90∘):(x,y)r↦(y,−x)r(O,270∘):(x,y)r↦(y,−x) |
r−1(O,90∘)=r(O,−90∘)r−1(O,−270∘)=r(O,270∘)r−1(O,180∘)=r(O,180∘)r−1(O,−90∘)=r(O,90∘)r−1(O,270∘)=r(O,−270∘) |
|
Réflexion (Symétrie) |
sx:(x,y)s↦(x,−y)sy:(x,y)s↦(−x,y)s/:(x,y)s↦(y,x)s∖:(x,y)s↦(−y,−x) |
s−1x=sxs−1y=sys−1/=s/s−1∖=s∖ |
|
Homothétie |
h(O,k):(x,y)h↦(kx,ky) |
h−1(O,k)=h(1k,1k):(x,y)h↦(xk,yk) |
Les coniques (Sec. 5 TS-SN)
|
Coniques |
Équations canoniques |
Paramètres |
|---|---|---|
|
Cercle Lieu géométrique de tous les points situés à égale distance du centre. |
x2+y2=r2 (x−h)2+(y−k)2=r2 |
r: rayon (h,k): Centre du cercle |
|
Ellipse Lieu géométrique de tous les points dont la somme des distances aux deux foyers est constante. |
x2a2+y2b2=1 (x−h)2a2+(y−k)2b2=1 |
a=Axe horizontale2b=Axe verticale2 (h,k): Centre de l'ellipse |
|
Hyperbole Lieu géométrique de tous les points dont la valeur absolue de la différence de la distance aux foyers est constante. |
x2a2−y2b2=±1 (x−h)2a2−(y−k)2b2=±1 |
Asymptotes : y=ba(x−h)+ky=−ba(x−h)+k (h,k): Centre de l'hyperbole |
|
Parabole Lieu géométrique de tous les points situés à égale distance de la directrice et du foyer |
(x−h)2=4c(y−k) (y−k)2=4c(x−h) |
|c|:Distance foyer-directrice2 (h,k): Sommet de la parabole |
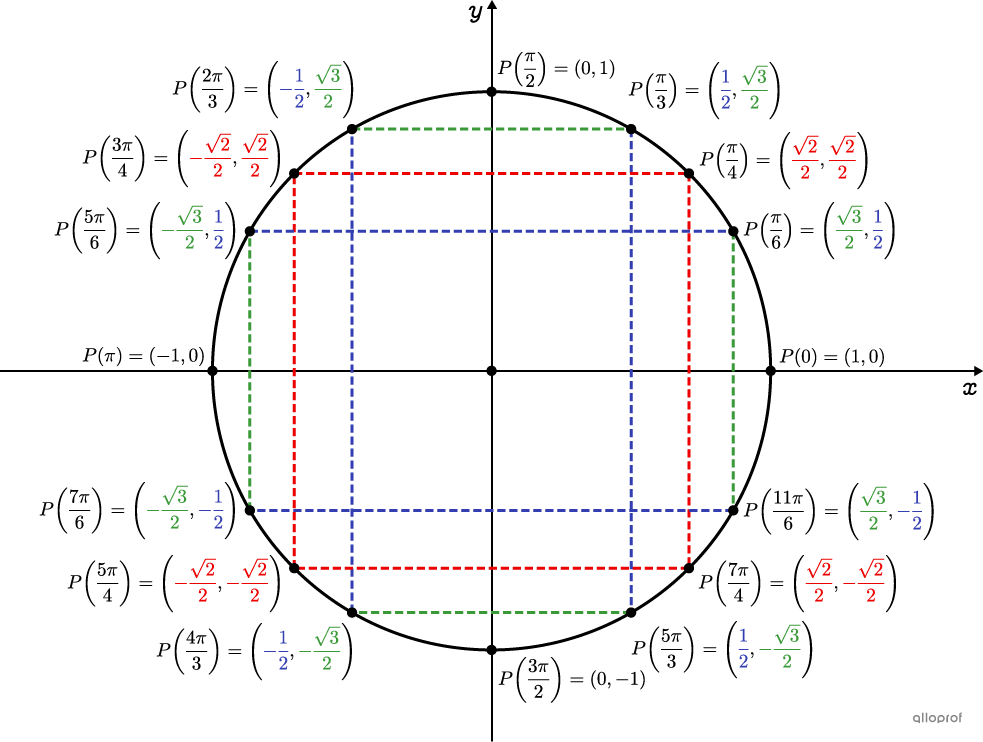
Le cercle trigonométrique (Sec. 5 TS-SN)
P(θ)=(cosθ,sinθ)
Probabilités et statistiques
Probabilités d’événements (Sec. 1 à 5)
|
Concepts |
Formules |
|---|---|
|
Probabilité |
Probabilité=Nbr de cas favorablesNbr de cas possibles |
|
Probabilité complémentaire |
P(A′)=1−P(A) |
|
Probabilité d'événements mutuellement exclusifs |
P(A∪B)=P(A)+P(B) |
|
Probabilité d'événements non mutuellement exclusifs |
P(A∪B)=P(A)+P(B)−P(A∩B) |
|
Probabilité conditionnelle |
P(B∣A)=PA(B)=P(B∩A)P(A) |
|
Espérance de gain |
E[Gain]=Probabilité de gagner×Gain net+Probabilité de perdre×Perte nette |
|
Espérance mathématique |
E[X]=x1P(x1)+x2P(x2)+…+xnP(xn)où les résultats possibles de X sont les valeurs x1,…,xn. |
Mesures de tendance centrale (Sec. 3)
|
Mesures |
Données non regroupées |
Données condensées |
Données regroupées |
|---|---|---|---|
|
Moyenne |
¯x=∑xin |
¯x=∑xinin |
¯x=∑minin |
|
Médiane |
Rangmédiane=(n+12)Si n est impair, on obtient directement la médiane. Si n est pair, on obtient la médiane en faisant la moyenne des deux données centrales. |
Rangmédiane=(n+12)Si n est impair, on obtient directement la médiane. Si n est pair, on obtient la médiane en faisant la moyenne des deux données centrales. |
Classe médiane : La classe contenant la médiane. On estime souvent la médiane d'une distribution à données regroupées en calculant le milieu de la classe médiane. |
|
Mode |
La donnée la plus fréquente |
La valeur avec le plus grand effectif |
Classe modale : La classe ayant le plus grand effectif |
Mesures de dispersion (Sec. 2-3-4 CST-TS)
|
Mesures |
Données non regroupées |
Données condensées |
Données regroupées |
|---|---|---|---|
|
Étendue |
E=xmax−xmin |
E=ValeurMax−ValeurMin |
E=Bornesup−Borneinf |
|
Étendue Interquartile |
EI=Q3−Q1 |
EI=Q3−Q1 |
EI=Q3−Q1 |
|
Intervalle semi-interquartile |
Q=EI2=Q3−Q12 |
Q=EI2=Q3−Q12 |
Q=EI2=Q3−Q12 |
|
Écart moyen |
EM=∑∣xi−¯x∣n |
EM=∑ni∣Xi−¯x∣n |
EM=∑ni∣mi−¯x∣n |
|
Écart type |
σ=√∑(xi−¯x)2n |
σ=√∑ni(Xi−¯x)2n |
σ=√∑ni(mi−¯x)2n |
Mesures de position (Sec. 4 CST)
|
Mesures |
Formules |
|---|---|
|
Rang cinquième |
R5(x)≈(Nbre de données supérieures à x+Nbre de données égales à x2Nbre total de données)×5Si le résultat n'est pas un nombre entier, on arrondit à l'entier supérieur. |
|
Rang centile |
R100(x)≈(Nbre de données inférieures à x+Nbre de données égales à x2Nbre total de données)×100Si le résultat n'est pas un nombre entier, on arrondit à l'entier supérieur, sauf si celui-ci est 99. |
Coefficient de corrélation (Sec. 4)
|
Calcul du coefficient de corrélation dans le plan cartésien |
|
|---|---|
|
r≈±(1−lL)où L représente la longueur et l, la largeur du rectangle englobant le nuage de points. Le signe de r dépend du sens du nuage de points. |
|
|
Interprétation du coefficient de corrélation |
|
| Près de 0 | Lien nul entre les variables |
| Près de -0,5 ou de 0,5 | Lien faible entre les variables |
| Près de -0,75 ou de 0,75 | Lien moyen entre les variables |
| Près de -0,87 ou de 0,87 | Lien fort entre les variables |
| Égal à -1 ou à 1 | Lien parfait entre les variables |
Dans cette page
- Haut de page
- Arithmétique et algèbre
- Exprimer un nombre en pourcentage (Sec. 1-2)
- Les propriétés des opérations (Sec. 1-2)
- Les fonctions réelles (Sec. 3-4-5)
- Les fonctions exponentielles et logarithmiques (Sec. 4 CST-TS et 5 TS-SN)
- Les fonctions trigonométriques (Sec. 5 TS-SN)
- Les identités trigonométriques (Sec. 5 TS-SN)
- Géométrie
- La conversion des unités de mesure (Sec. 1-2-3)
- Le périmètre et l'aire des figures planes (Sec. 1-2-4)
- Les mesures dans le cercle (Sec. 1-2 et 5 TS)
- Les mesures dans les polygones (Sec. 1-2)
- L'aire et le volume des solides (Sec. 2-3)
- Les mesures dans les triangles rectangles (Sec. 3-4)
- Les rapports trigonométriques (Sec. 4)
- Les figures et les solides semblables (Sec. 3)
- Les vecteurs (Sec. 5 TS-SN)
- Géométrie analytique
- Les droites dans le plan cartésien (Sec. 3-4)
- Les règles des transformations géométriques et leur réciproque dans le plan cartésien (Sec. 5 TS)
- Les coniques (Sec. 5 TS-SN)
- Le cercle trigonométrique (Sec. 5 TS-SN)
- Probabilités et statistiques
- Probabilités d’événements (Sec. 1 à 5)
- Mesures de tendance centrale (Sec. 3)
- Mesures de dispersion (Sec. 2-3-4 CST-TS)
- Mesures de position (Sec. 4 CST)
- Coefficient de corrélation (Sec. 4)















































