La loi de Hess
La loi de Hess stipule que si une réaction représente à elle seule deux ou plusieurs autres réactions, la chaleur qu’elle dégage ou absorbe est égale à la somme des chaleurs dégagées ou absorbées par les autres réactions.
Certaines réactions chimiques se produisent en apparence de façon très simple. Toutefois, elles sont souvent le fruit d'un processus complexe nécessitant de nombreuses réactions intermédiaires pour passer des réactifs aux produits. Cette suite de réactions simples forme un mécanisme réactionnel qui est résumé par l'équation balancée d'une réaction complexe. La chaleur globale de la réaction complexe peut être déterminée mathématiquement à l'aide de la loi de Hess, aussi nommée loi d'additivité des enthalpies.
Le mécanisme réactionnel
Un mécanisme réactionnel est une suite chronologique de réactions intermédiaires qui conduisent des réactifs aux produits d'une réaction complexe.
On représente généralement une réaction chimique par une équation balancée contenant des réactifs qui se transforment en produits. Cette représentation simple ne donne toutefois aucune information sur le déroulement de la réaction chimique. En effet, dans la majorité des réactions chimiques, les réactifs ne sont pas directement transformés en produits. Ils forment plutôt une série de substances intermédiaires qui mèneront ultimement aux produits finaux. Ainsi, on peut décomposer une réaction complexe en une succession de réactions intermédiaires. Cela correspond à un mécanisme réactionnel.
On peut représenter un mécanisme réactionnel par la somme d'une série de réactions intermédiaires. On obtient alors l'équation de la réaction complexe. Cette équation permet de résumer le mécanisme réactionnel de la réaction complexe sans toutefois indiquer les étapes intermédiaires qu'elle contient.
La formation de dioxyde d'azote à partir d'oxyde d'azote et de dioxygène est une réaction complexe qui comporte deux étapes intermédiaires.
2 NO(g)→N2O2(g)N2O2(g)+O2(g)→2 NO2(g)¯42 NO(g)+O2(g)¯→2 NO2(g)4
On peut aussi représenter un mécanisme réactionnel à l'aide d'un diagramme énergétique. Dans un tel diagramme, chaque étape est une réaction intermédiaire dans laquelle le produit de la première réaction devient le réactif de la seconde, et ainsi de suite jusqu'à la production des produits finaux. Chaque réaction possède une énergie d'activation et une variation d'enthalpie qui lui sont propres.
Le mécanisme réactionnel d'une réaction complexe hypothétique allant du réactif A au produit E se déroule en quatre étapes distinctes.
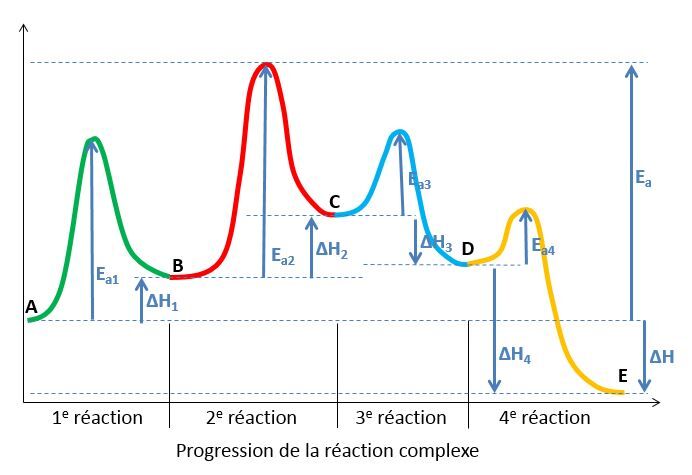
Important!
L'étape qui possède la plus grande énergie d'activation est celle qui détermine la vitesse du mécanisme réactionnel. En effet, plus l'énergie d'activation est importante et plus l'étape en question se déroule lentement. Dans le graphique ci-dessus, la deuxième réaction est l'étape la plus lente puisqu'elle possède la plus grand énergie d'activation.
La loi de Hess
La loi de Hess indique que, lorsqu'une réaction peut être décomposée en plusieurs réactions élémentaires, la variation d'enthalpie globale de la réaction complexe est égale à la somme algébrique des variations d'enthalpie de chacune des réactions intermédiaires.
En 1840, le chimiste suisse (1802-1850) Germain Henri Hess a élaboré une méthode permettant de prédire la variation d'enthalpie engendrée par des réactions chimiques. Cette méthode algébrique, nommée loi de Hess, s'avère très utile entre autres dans les situations où il est impossible d'effectuer certaines réactions en laboratoire. C'est notamment le cas des réactions trop rapides, trop lentes ou trop violentes.
Lors de l'élaboration de la loi, Hess a remarqué que la variation d'enthalpie d'une réaction est la même, que cette réaction se déroule en une ou en plusieurs étapes. Ainsi, la variation ne dépend que des réactifs et des produits et est indépendante du mécanisme de la réaction et du nombre d'étapes intermédiaires nécessaires au déroulement de la réaction complète. On peut exprimer mathématiquement cette loi par l'équation suivante:
△H=△H1+△H2+△H3+...
où
△H représente la variation d'enthalpie globale en kJ/mol
△H1,△H2,△H3 représentent la variation d'enthalpie de chacune des réactions intermédiaires de la réaction globale en kJ/mol
L'enthalpie d'une réaction demeure donc identique, que la réaction passe directement des réactifs aux produits ou qu'elle se déroule en plusieurs étapes. Par exemple, la formation du dioxyde de carbone peut se dérouler selon deux mécanismes différents.
Deux mécanismes sont responsables de la formation du dioxyde de carbone:
1. Le dioxyde de carbone peut directement être produit par la réaction du carbone au contact du dioxygène. On résume cette réaction de la façon suivante:
C_{(s)} + O_{2(g)} \rightarrow CO_{2(g)} \hspace {25 mm}ΔH = -393,5 \:\text{kJ/mol}
2. Cette réaction peut aussi se dérouler en deux étapes. \begin{align*} C_{(s)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{(g)}}} & &\Delta H_1= -110,5\:\text{kJ/mol}\\ \enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{(g)}}} + 1/2\ O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_2= -283,0\:\text{kJ/mol}\\ \hline {\phantom{CO_2^4} C_{(s)} + O_{2(g)} \quad} &{\phantom{^4}\;\rightarrow \quad CO_{2(g)}} & &{\Delta H= -393,5\:\text{kJ/mol}\phantom{^4}} \end{align*}
On voit que, peu importe le mécanisme réactionnel considéré, le résultat final est le même, c'est-à-dire la production d'une mole de dioxyde de carbone à partir d'une mole de carbone solide et d'une mole de dioxygène gazeux. Aussi, la variation d'enthalpie est la même dans les deux mécanismes.
Pour déterminer la chaleur d'une réaction par la loi de Hess, on doit suivre certaines règles.
Règle
- Les termes identiques situés du même côté de l'équation s'additionnent.
- Les termes identiques situés de part et d'autre de l'équation se soustraient.
- Si on inverse une équation, on doit aussi inverser le signe du \triangle H.
- Si on modifie les coefficients d'une équation chimique en les multipliant ou en les divisant par un facteur commun, on doit aussi multiplier ou diviser la valeur du \triangle H par ce même facteur commun.
Afin d'aider au calcul de la chaleur d'une réaction à l'aide de la loi de Hess, on peut suivre les étapes énumérées ci-dessous. Évidemment, selon le cas, certaines de ces étapes ne seront pas toujours nécessaires.
Règle
Étapes à suivre pour calculer la chaleur d'une réaction à l'aide de la loi de Hess
- Écrire l'équation globale balancée.
- Choisir les équations intermédiaires pertinentes.
- Réorganiser les équations en les inversant ou en les multipliant.
- Additionner les équations ainsi que les chaleurs qui leur sont associées.
- Convertir la valeur obtenue selon les exigences du problème à résoudre.
Quelle est la chaleur molaire de la synthèse du méthane à partir du carbone solide et du dihydrogène gazeux?
1. Équation globale de la réaction
C_{(s)} + 2\ H_{2(g)} \rightarrow CH_{4(g)}
2. Équations intermédiaires de la réaction
\begin{align*} &1)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_1= -394,1\:\text{kJ/mol}\\ &2)&\ H_{2(g)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad H_2O_{(g)} & &\Delta H_2= -242,2\:\text{kJ/mol}\\ &3)&\ CH_{4(g)} + 2\ O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} + 2\ H_2O_{(g)} & &\Delta H_3= -803,6\:\text{kJ/mol} \end{align*}
3. Manipulations des équations intermédiaires
Il est nécessaire d'inverser la troisième réaction et de multiplier par un facteur de 2 la deuxième réaction. On obtient donc:
\begin{align*} &1)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_1= -394,1\:\text{kJ/mol}\\ &2)&\ 2\ H_{2(g)} + O_{2(g)} \quad &\rightarrow \quad 2\ H_2O_{(g)} & &\Delta H_2= -484,4\:\text{kJ/mol}\\ &3)&\ CO_{2(g)} + 2\ H_2O_{(g)} \quad &\rightarrow \quad CH_{4(g)} + 2\ O_{2(g)} & &\Delta H_3= +803,6\:\text{kJ/mol} \end{align*}
4. Addition des équations
\begin{align*} &1)&\ C_{(s)} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{O_{2(g)}}} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{2(g)}}} & &\Delta H_1= -394,1\:\text{kJ/mol}\\ &2)&\ 2\ H_{2(g)} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{O_{2(g)}}} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2 \: H_2O_{(g)}}} & &\Delta H_2= -484,4\:\text{kJ/mol}\\ &3)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{CO_{2(g)}}} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2\ H_2O_{(g)}}} \quad &\rightarrow \quad CH_{4(g)} + \enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{2\ O_{2(g)}}} & &\Delta H_3= +803,6\:\text{kJ/mol} \\ \hline &&\ C_{(s)} + 2\ {H_{2(g)}} \quad &\rightarrow \quad {CH_{4(g)}} & &\Delta H_{ }= -74,9\:\text{kJ/mol} \end{align*}
5. Réponse: La chaleur molaire de réaction est de -74,9\:\text{kJ/mol}.
Quelle est la chaleur de réaction de la combustion du propane?
1. Équation globale de la réaction
C_{3}H_{8(g)} + 5\ O_{2(g)} \rightarrow 3\ CO_{2(g)} + 4\ H_{2}O_{(g)}
2. Équations intermédiaires de la réaction
\begin{align*} &1)&\ H_{2(g)} + 1/2\ O_{2(g)} \quad &\rightarrow \quad H_2O_{(g)} & &\Delta H_1= -242,2\:\text{kJ/mol}\\ &2)&\ 3\ C_{(s)} + 4\ H_{2(g)} \quad &\rightarrow \quad C_3H_{8(g)} & &\Delta H_2= -103,8\:\text{kJ/mol}\\ &3)&\ C_{(s)} + O_{2(g)} \quad &\rightarrow \quad CO_{2(g)} & &\Delta H_3= -394,1\:\text{kJ/mol} \end{align*}
3. Manipulation des équations intermédiaires
On doit multiplier la première équation par un facteur de 4, inverser la deuxième équation et finalement multiplier la troisième réaction par un facteur de 3.
\begin{align*} &1)&\ 4\ H_{2(g)} + 2\ O_{2(g)} \quad &\rightarrow \quad 4\ H_2O_{(g)} & &\Delta H_1= -968,8\:\text{kJ/mol}\\ &2)&\ C_3H_{8(g)} \quad &\rightarrow \quad 3\ C_{(s)} + 4\ H_{2(g)} & &\Delta H_2= +103,8\:\text{kJ/mol}\\ &3)&\ 3\ C_{(s)} + 3\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} & &\Delta H_3= -1\:182,3\:\text{kJ/mol} \end{align*}
4. Addition des équations
\begin{align*} &1)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{4\ H_{2(g)}}}+ 2\ O_{2(g)} \quad &\rightarrow \quad 4\ H_2O_{(g)} & &\Delta H_1= -968,8\:\text{kJ/mol}\\ &2)&\ C_3H_{8(g)} \quad &\rightarrow \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{3\ C_{(s)}}} + \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{4\ H_{2(g)}}} & &\Delta H_2= +103,8\:\text{kJ/mol}\\ &3)&\ \quad\enclose{updiagonalstrike}[mathcolor="red"]{\color{black}{3\ C_{(s)}}} + 3\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} & &\Delta H_3= -1\:182,3\:\text{kJ/mol} \\ \hline &&C_{3}H_{8(g)} + 5\ O_{2(g)} \quad &\rightarrow \quad 3\ CO_{2(g)} + 4\ H_{2}O_{(g)} & &\Delta H_{ }= -2\:047,3\:\text{kJ/mol} \end{align*}
5. Réponse: La chaleur de réaction est de -2\:047,3\:\text{kJ/mol}.
Exercices
















































