
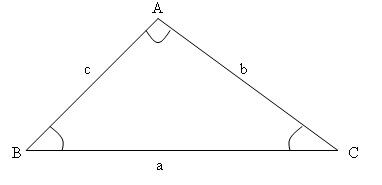
La loi des sinus
Secondaire 4-5
La loi des sinus est une formule qui établit un lien entre les rapports des sinus des angles et les mesures de leurs côtés opposés. Elle est valable pour tous les triangles.
La loi des sinus permet de trouver la mesure d'un côté ou d'un angle dans un triangle quelconque. Pour ce faire, il faut connaitre la mesure d'un angle, de son côté opposé et d'un autre côté ou d'un autre angle.
La loi des sinus prend la forme qui suit :
Remarque : On peut également écrire la formule de la façon suivante :
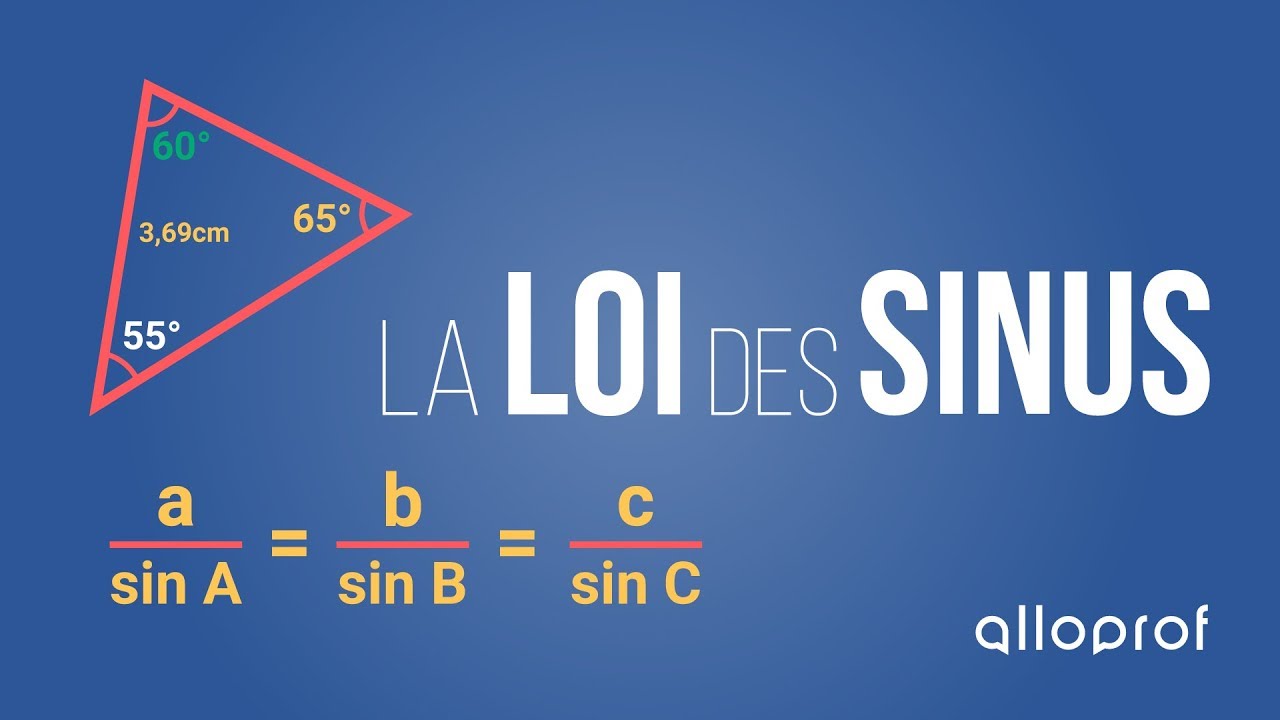
La loi des sinus
Important!
On utilise cette loi quand on connait la mesure d’un angle et celle de son côté opposé ainsi que n’importe quelle autre valeur de côté (à gauche) ou d’angle (à droite) du triangle.
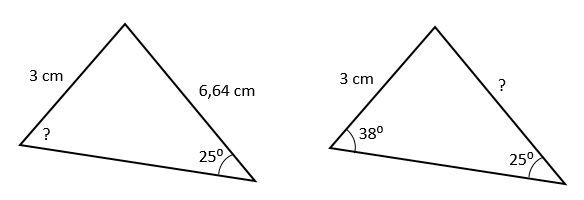
En bref, il faut une paire (côté, angle) qui est complète.
Quelle est la mesure du côté opposé à l’angle de 35° ?
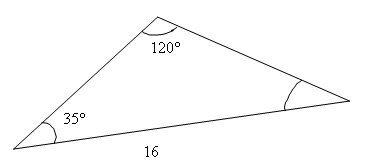
On pose premièrement l’équation qui met en relation le côté opposé à l’angle de 35° avec les données connues :
Le côté opposé à l'angle de 35º mesure donc 10,6 unités.
La loi des sinus : les angles obtus
Situation avec un angle obtus
Quelle est la mesure de l'angle opposé au côté ?
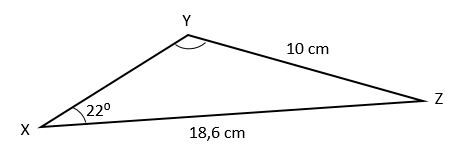
On utilise la loi des sinus pour déterminer la valeur manquante.
Toutefois, lorsqu'on regarde l'angle Y dans le schéma ci-dessus, on constate qu'il s'agit d'un angle obtus. Il faut donc trouver l'angle obtus qui possède un sinus équivalent à l'angle de 44,2º. Pour ce faire :
L'angle Y a une valeur de 135,8º.
Attention!
Il faut toujours vérifier s'il s'agit d'un angle obtus ou aigu lorsqu'on recherche la mesure d'un angle. S'il s'agit d'un angle aigu, la réponse est obtenue directement. Toutefois, s'il s'agit d'un angle obtus, il faut soustraire la réponse obtenue de 180 afin de déterminer la vraie valeur de l'angle.
Pour valider ta compréhension de la trigonométrie de façon interactive, consulte la MiniRécup suivante :

Exercices
Références
Dans cette page















































